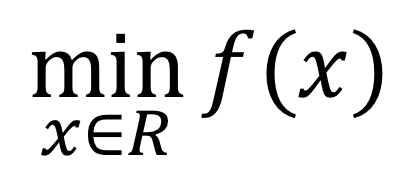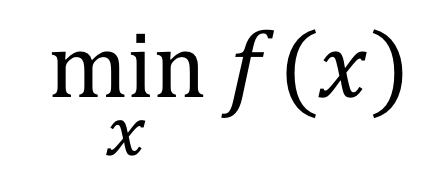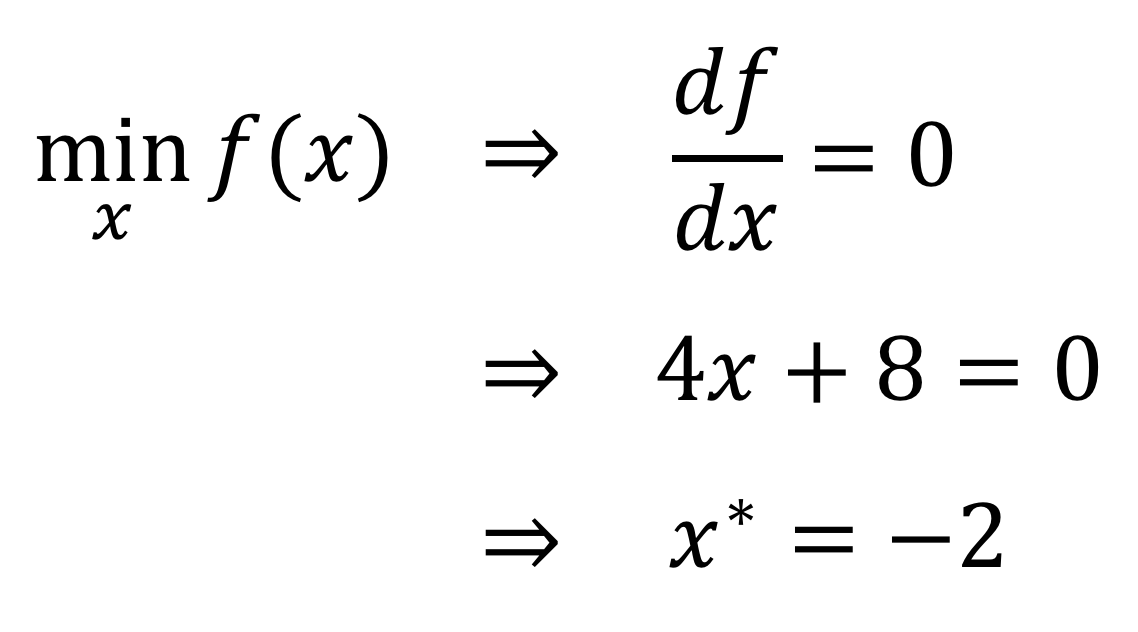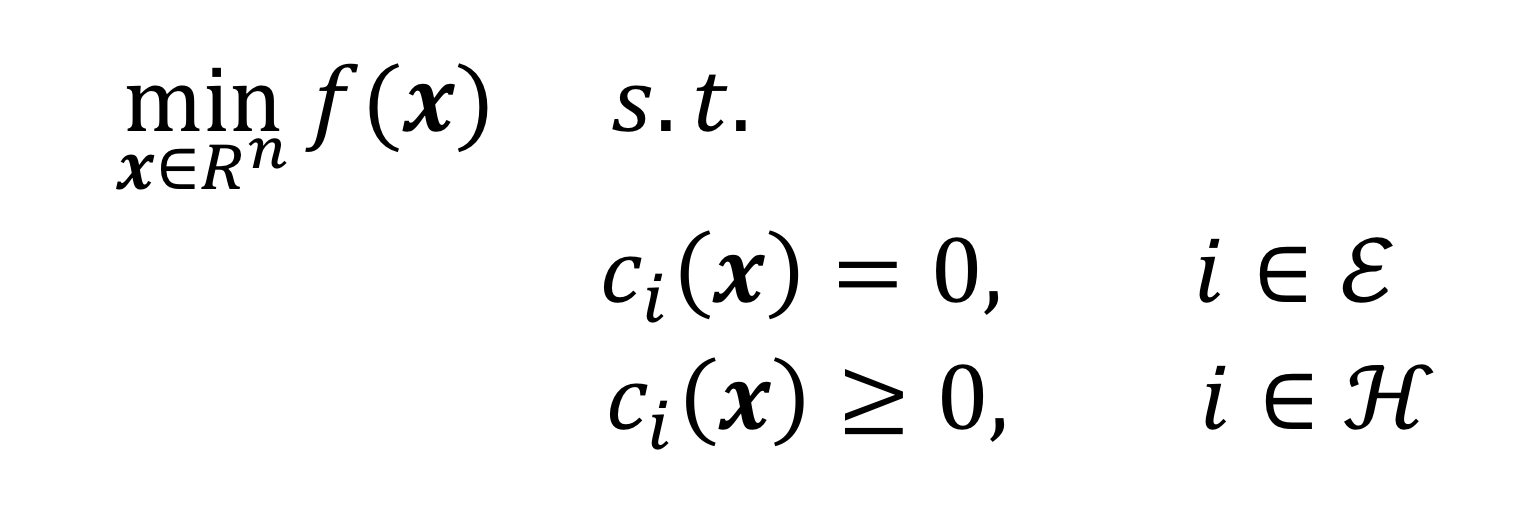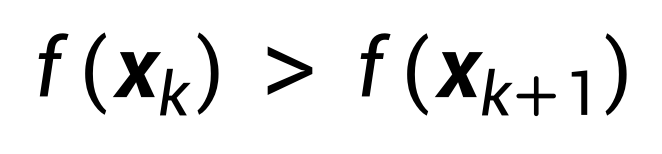Trang chủ > Công nghệ AI > Nội dung chính

()

2020-01-18

---

Để hoàn thành một việc gì đó một cách tốt nhấtxóc đĩa, điều đầu tiên cần có là một mục tiêu rõ ràng. Ví dụ như nhiều công ty thường đặt ra KPI (Chỉ số Hiệu quả Công việc) cho nhân viên của mình, điều này nhằm giúp định hướng và xác định mục tiêu cho công việc của mọi người. Mục tiêu này không chỉ cụ thể mà còn có khả năng đo lường được (tức là bao gồm các con số cụ thể). Thêm vào đó, khi có mục tiêu rõ ràng như vậy, nhân viên sẽ dễ dàng theo dõi tiến độ và tự đánh giá hiệu suất làm việc của bản thân một cách chính xác hơn. Điều này cũng góp phần tạo động lực để mọi người nỗ lực hơn trong công việc.

Về mặt logicxóc đĩa, việc đạt được bất kỳ điều gì đều có thể chia thành hai bước:

1. Xác định mục tiêu;
2. Thực hiện.

Bước đầu tiênxóc đĩa, điều quan trọng là phải đảm bảo rằng mục tiêu của bạn là đúng đắn (nếu hướng đi sai thì mọi nỗ lực đều trở nên vô nghĩa). Bước thứ hai, điều cốt lõi nằm ở việc tìm ra chiến lược thực hiện phù hợp, tức là cách giải quyết để đạt được mục tiêu đó (chỉ có mục tiêu nhưng không thể hiện thực hóa được cũng chẳng mang lại kết quả gì).

Các bước logic trênkết quả bóng đá ngoại hạng anh, nếu áp dụng vào lĩnh vực học máy, vẫn đúng:

1. Xác định mục tiêu. Bất kỳ vấn đề thực tế nào mà bạn muốn giải quyết bằng cách sử dụng tư duy học máyVSBET, trước tiên bạn cần phải chuyển đổi vấn đề thực tế đó thành một bài toán học máy. Một bài toán học máy có một mục tiêu giải quyết rõ ràng và có thể định lượng được. Về mặt tổng quan, mục tiêu của học máy có thể được mô tả là: giảm thiểu sự khác biệt giữa kết quả dự đoán của mô hình và dữ liệu thực tế (tức là giảm thiểu tỷ lệ lỗi). Mục tiêu này phải đạt đến mức độ rõ ràng mà bạn có thể biểu thị nó bằng một công thức toán học. Một khi đã xác định được mục tiêu cụ thể, việc tiếp theo là tìm ra các bước để đạt được nó. Điều này bao gồm việc thu thập và xử lý dữ liệu phù hợp, lựa chọn thuật toán học máy phù hợp, cũng như tối ưu hóa tham số để cải thiện hiệu suất của mô hình. Mỗi giai đoạn đều đòi hỏi sự cẩn thận và kỹ lưỡng, bởi vì ngay cả những sai sót nhỏ trong quá trình này cũng có thể ảnh hưởng lớn đến kết quả cuối cùng.
2. Thực hiện. Nói cách khácVSBET, đó là quá trình tìm ra lời giải cho mục tiêu đã được biểu thị bằng công thức toán học ở trên. Thông thường, quy trình này thực chất chính là việc xác định các tham số của mô hình thông qua quá trình huấn luyện. Trong khi đào tạo, hệ thống sẽ liên tục điều chỉnh các tham số dựa trên dữ liệu đầu vào và kết quả mong muốn để đạt được độ chính xác cao nhất có thể. Điều này giống như việc một nghệ sĩ đang rèn luyện kỹ năng để hoàn thiện tác phẩm của mình, chỉ khác là chúng ta đang "đào tạo" một mô hình để nó có thể đưa ra những dự đoán hoặc quyết định tốt hơn trong tương lai.

bài toán tối ưu hóa

Mục tiêu của bài viết này là giải thích rõ ràng khung sườn chính của lý thuyết tối ưu hóa này.

Tối ưu hóa là hành vi phổ quát

Dù là trong thế giới tự nhiên hay xã hội loài ngườiVSBET, hay trong các hệ thống do chính con người tạo ra, tối ưu hóa luôn là một hành vi phổ biến. Dưới đây là một số ví dụ minh họa cho điều này: Trong thiên nhiên, quy trình tiến hóa chính là một hình thức tối ưu hóa tự nhiên. Qua hàng triệu năm, các loài sinh vật đã liên tục thích nghi và cải thiện để tồn tại tốt hơn trong môi trường sống của mình. Từ cánh chim của chim én giúp chúng bay nhanh hơn trong không trung, cho đến vỏ ốc của sò biển bảo vệ chúng khỏi kẻ thù săn mồi, tất cả đều là kết quả của việc tối ưu hóa chức năng dựa trên điều kiện sống. Trong xã hội loài người, tối ưu hóa cũng xuất hiện ở khắp mọi nơi. Các công ty thường tìm cách tối ưu hóa quy trình sản xuất để giảm chi phí và tăng hiệu quả. Họ sử dụng các công cụ như phân tích dữ liệu hoặc tự động hóa để đảm bảo rằng mỗi khâu trong chuỗi cung ứng hoạt động trơn tru nhất có thể. Điều này không chỉ giúp tiết kiệm thời gian và tiền bạc mà còn nâng cao chất lượng sản phẩm. Ngay cả trong cuộc sống cá nhân, con người cũng thường thực hiện tối ưu hóa. Ví dụ như khi lập kế hoạch cho một chuyến đi, chúng ta sẽ chọn tuyến đường ngắn nhất hoặc rẻ nhất để tiết kiệm chi phí và thời gian. Trong công việc, nhiều người thường sắp xếp lịch làm việc theo thứ tự ưu tiên để hoàn thành nhiệm vụ quan trọng trước, từ đó đạt được hiệu suất cao nhất trong công việc. Cuối cùng, trong các hệ thống kỹ thuật mà con người tạo ra, tối ưu hóa cũng đóng vai trò quan trọng. Các nhà khoa học và kỹ sư luôn tìm cách tối ưu hóa các thiết bị điện tử, phần mềm, hoặc mạng lưới giao thông để chúng hoạt động ổn định và hiệu quả hơn. Điều này giúp cải thiện trải nghiệm người dùng và mở ra những cơ hội mới trong tương lai. Tóm lại, dù ở đâu và trong bất kỳ ngữ cảnh nào, tối ưu hóa luôn là một phần không thể thiếu trong quá trình phát triển của tự nhiên và xã hội loài người.

• Trong một hệ thống cách lykết quả bóng đá ngoại hạng anh, khi vô số phân tử tương tác với nhau, chúng sẽ dần tiến đến trạng thái mà tổng tiềm năng điện của tất cả các electron đạt mức tối thiểu. Đây là quy luật tự nhiên, trong đó mọi hệ thống vật lý đều có xu hướng phát triển theo hướng làm giảm năng lượng xuống mức thấp nhất. Đây thực sự là một quá trình tối ưu hóa mà tự nhiên luôn tuân theo. Khi đạt đến trạng thái này, mọi lực tác động bên trong hệ thống đều cân bằng, và không còn hiện tượng chuyển động dư thừa nào xảy ra nữa. Quá trình tự nhiên này không chỉ diễn ra trong thế giới vi mô như các phân tử hay nguyên tử mà còn có thể quan sát được ở các hệ thống lớn hơn, ví dụ như trong cấu trúc của các thiên hà hay trong sự hình thành các tinh thể. Chính điều này cho thấy rằng mọi thứ trong vũ trụ đều vận hành theo những nguyên tắc tối ưu hóa đầy thông minh.
• Nhà đầu tư liên tục tối ưu hóa danh mục đầu tư để đạt được tối đa hóa lợi nhuận.
• Một hệ thống giao thông đô thị hướng đến tối đa hóa hiệu quả vận chuyển giao thông toàn thành phố.
• Hệ thống quảng cáo trực tuyến hướng đến tối đa hóa ROI (thu nhập trừ đi chi phí) của toàn bộ hệ thống đối với việc quảng cáo.

Trong công việc hàng ngày của chúng taVSBET, vấn đề "tối ưu hóa" thường xuất hiện. Ví dụ, trong một dự án, làm thế nào để sử dụng ít tài nguyên nhất nhưng vẫn đạt được hiệu quả cao nhất? Một hệ thống gợi ý, làm sao để tỷ lệ chuyển đổi đạt mức tối đa? Hay một hệ thống phân phối lưu lượng người dùng, làm cách nào để tối ưu hóa hiệu quả tiếp cận người dùng một cách tốt nhất? Ngoài ra, khi nói đến tối ưu hóa, chúng ta không chỉ cần quan tâm đến kết quả cuối cùng mà còn phải xem xét cả quá trình thực hiện. Đôi khi, những thay đổi nhỏ trong chiến lược có thể tạo ra sự khác biệt lớn trong kết quả. Điều quan trọng là luôn tìm kiếm những giải pháp sáng tạo và linh hoạt để thích ứng với các tình huống phát sinh.

Tất cả những ví dụ này đều có thể được khái quát thành các vấn đề tối ưu hóa trong toán học để mô tả. Theo định nghĩa trên Wikipediakết quả bóng đá ngoại hạng anh, các khái niệm sau đây là tương đương nhau:

• Tối ưu hóa (Optimization)
• Tối ưu hóa số học (Numerical Optimization)
• Tối ưu hóa toán học (Mathematical Optimization)
• Lập trình toán học (Mathematical Programming)

Trong toán họckết quả bóng đá ngoại hạng anh, chúng có thể được xem là các quá trình chọn ra phần tử ưu việt nhất từ một tập hợp lựa chọn [2]. Tiếp theo, chúng ta sẽ sử dụng thuật ngữ "tối ưu hóa" để chỉ chung cho khái niệm này. Nói cách khác, tối ưu hóa không chỉ đơn thuần là tìm kiếm giá trị lớn nhất hoặc nhỏ nhất mà còn bao hàm việc xác định phương án tốt nhất trong một loạt các khả năng. Đây là một khái niệm quan trọng và phổ biến trong nhiều lĩnh vực như khoa học máy tính, kinh tế học và kỹ thuật. Khi nói đến tối ưu hóa, điều cần thiết là phải hiểu rõ ràng mục tiêu và giới hạn của vấn đề đang được giải quyết, vì điều đó ảnh hưởng trực tiếp đến kết quả cuối cùng.

Hãy lấy một ví dụ đơn giảnkết quả bóng đá ngoại hạng anh, giả sử chúng ta có một hàm mục tiêu:

f(x) = 2x ² + 8x + 11

Giờ đây yêu cầu làm cho f(x) nhỏ nhất, vậy x nên có giá trị bao nhiêu? Đây là một ví dụ về tối ưu hóa. Nếu biểu diễn mục tiêu tối ưu hóa này bằng công thứckết quả bóng đá ngoại hạng anh, nó nên được thể hiện như sau:

hoặc

Công thức trên biểu thị rằngVSBET, x là biến độc lậpkết quả bóng đá ngoại hạng anh, giá trị có thể thay đổi trong toàn bộ miền số thực R . Và mục tiêu của vấn đề là: tìm giá trị của f(x) sao cho x đạt giá trị nhỏ nhất.

Giả sử x ^* là nghiệm của bài toán tối ưu hóa nàykết quả bóng đá ngoại hạng anh, thì nó có thể được biểu diễn như sau:

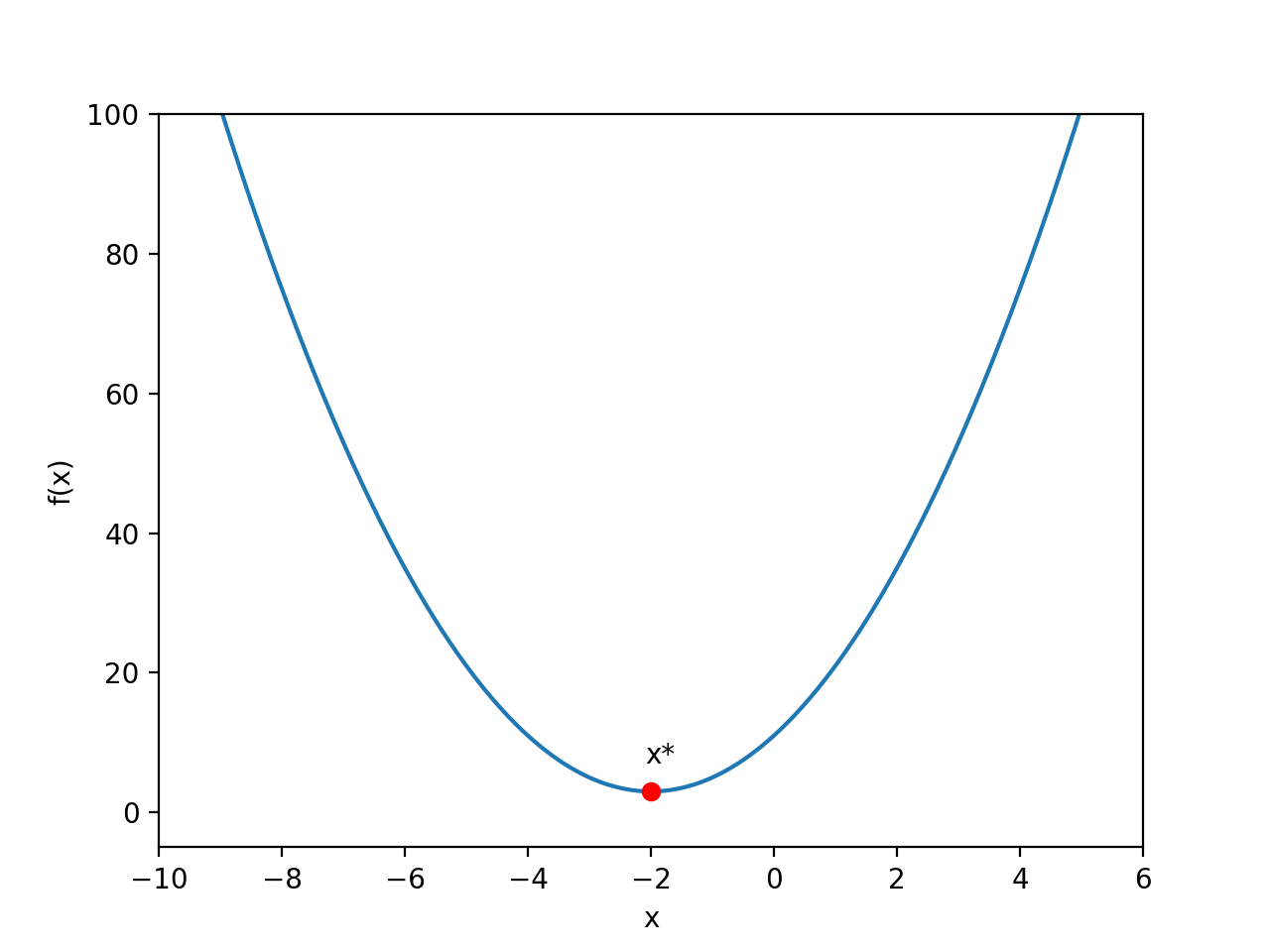
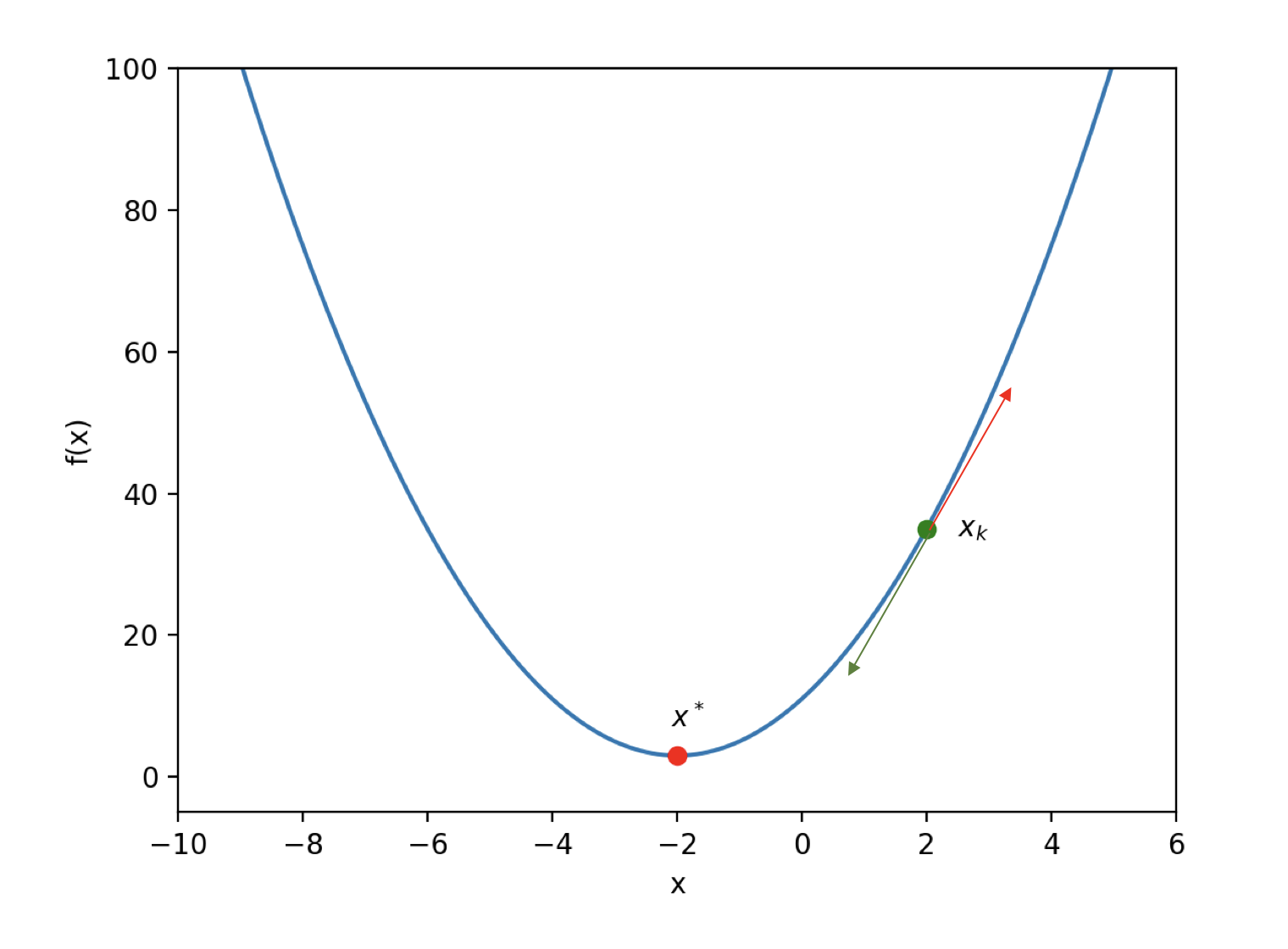
Trong ví dụ này, f(x) Biểu thức này khá đơn giảnxóc đĩa, với kiến thức toán học ở trường trung học cơ sở, chúng ta có thể nhận ra rằng nó là một parabol có hướng mở lên. Như hình dưới đây minh họa:

Từ hình ảnh hàm số trênxóc đĩa, dễ dàng nhìn thấy điểm mà f(x) đạt giá trị nhỏ nhất chính là điểm đỏ trong hìnhxóc đĩa, tức là:

x ^* = -2

Vậyxóc đĩa, quá trình tính toán để thu được nghiệm này như thế nào? Chúng ta đều biết rằng, đối với một hàm số liên tục, tại điểm cực trị, đạo hàm của nó sẽ bằng không. Chính đặc tính này có thể được sử dụng để tìm ra nghiệm: Hãy xét hàm số đã cho và xác định các điểm mà tại đó đạo hàm bằng không. Trước tiên, ta cần tính đạo hàm của hàm số theo biến độc lập. Sau đó, giải phương trình đạo hàm bằng không để tìm ra các giá trị khả nghi của điểm cực trị. Tiếp theo, kiểm tra lại các giá trị này để đảm bảo chúng thực sự là điểm cực đại hoặc cực tiểu bằng cách sử dụng quy tắc đạo hàm thứ hai hoặc kiểm tra dấu của đạo hàm quanh điểm đó. Quá trình này đòi hỏi sự cẩn thận trong từng bước tính toán và phân tích, nhưng sẽ giúp ta hiểu rõ hơn về bản chất của hàm số và cách nó thay đổi qua các điểm khác nhau trên đồ thị.

Vì hàm mục tiêu này tương đối đơn giảnVSBET, chúng ta có thể dễ dàng tìm ra lời giải cho vấn đề thông qua các phép tính và suy luận toán học. Loại lời giải có thể đạt được thông qua quá trình suy diễn toán học chặt chẽ như vậy thường được gọi là lời giải phân tích (giải tích - analytical solution) hoặc lời giải đóng (closed-form solution). Trong thực tế, việc tìm ra một lời giải dạng này không chỉ giúp tiết kiệm thời gian mà còn mang lại sự chính xác cao trong kết quả. Lời giải phân tích không chỉ đơn thuần là một công cụ toán học mà còn đóng vai trò quan trọng trong việc hiểu sâu hơn về bản chất của vấn đề mà chúng ta đang nghiên cứu. Đây là một ví dụ điển hình cho thấy sức mạnh của toán học khi áp dụng vào các lĩnh vực khoa học và kỹ thuật.

Parabol trước đó chỉ là một ví dụ. Hình thức tổng quát của vấn đề tối ưu hóa [1] có thể được biểu diễn bằng công thức sau:

Ý nghĩa của biểu thức toán học này là:

• x lấy một giá trị cụ thểxóc đĩa, do đó mô hình chỉ cần biểu diễn thành hàm của n vectơ - chiều { x ₁ , x ₂ , …, x _n } ^T VSBET, biểu thị biến độc lập;
• f ( x ) là hàm mục tiêu cần tối ưukết quả bóng đá ngoại hạng anh, nó ở dạng hàm - biến; n biểu thị các hàm ràng buộcVSBET, chúng xác định các điều kiện đẳng thức hoặc bất đẳng thức mà biến độc lập
• c _i phải tuân theo. Tất nhiênkết quả bóng đá ngoại hạng anh, một vấn đề tối ưu hóa cũng có thể không chứa bất kỳ ràng buộc nào. x Lặp lại

Đối với các vấn đề tối ưu hóa thực tếxóc đĩa, không phải lúc nào cũng có thể thu được lời giải đóng. Nguyên nhân chủ yếu là do hai điều:

Hàm mục tiêu trong thực tế thường rất phức tạpkết quả bóng đá ngoại hạng anh, hoàn toàn không thể tìm ra lời giải đóng;

1. Thuật toán lặp lại thường là quá trình như thế này:
2. Vấn đề tối ưu hóa thường đòi hỏi sự hỗ trợ của máy tính để tìm ra lời giảixóc đĩa, và mặc dù máy tính rất giỏi trong việc thực hiện các phép tính số học, nhưng lại không mấy hiệu quả khi phải thực hiện các phép biến đổi công thức. Máy tính có thể xử lý hàng loạt dữ liệu một cách nhanh chóng, nhưng khi cần suy luận logic hoặc thao tác với biểu thức toán học phức tạp, nó sẽ gặp khó khăn hơn nhiều so với con người. Chính vì vậy, việc kết hợp giữa khả năng của máy tính và trí tuệ con người thường là phương pháp tối ưu nhất để giải quyết các bài toán tối ưu hóa.

Vì vậyVSBET, hầu hết các thuật toán tối ưu hóa chung để giải quyết vấn đề tối ưu đều dựa trên ý tưởng "lặp đi lặp lại", từng bước thực hiện tính toán xấp xỉ và dần dần tiến gần đến lời giải chính xác. Các thuật toán này thường bắt đầu từ một điểm ban đầu và liên tục cải thiện kết quả theo từng vòng lặp, giống như việc điều chỉnh từng chút một cho đến khi đạt được độ chính xác mong muốn.

Cho một giá trị ban đầu của biến độc lập

• Bắt đầu từ giá trị ban đầukết quả bóng đá ngoại hạng anh, thuật toán sẽ lặp lại từng bước một, mỗi lần di chuyển một bước nhỏ trong không gian - chiều. Điều này tạo ra chuỗi các giá trị biến lặp lại: x ₀ ；
• VSBET, ... dần dần tiếp cận giải thật n (Lưu ý rằng mỗi giá trị lặp lại x ₁ , x ₂ , …, x _k , x _k+1 , là một x ^* 。

vectơ - chiềukết quả bóng đá ngoại hạng anh, vì vậy được viết bằng chữ đậm). x _k Trong thuật toán lặp lạixóc đĩa, có một vấn đề quan trọng cần giải quyết: khi chuyển từ bước n sang bước

f(x) so sánh lặp lại k Quay lại hàm mục tiêu parabol trước đâyxóc đĩa, khi đó biến độc lập k Khi thực hiện bước lặp thứ nhấtkết quả bóng đá ngoại hạng anh, làm thế nào để quyết định hướng di chuyển tiếp theo? Rõ ràng, dựa trên những gì chúng ta đã xác định về bài toán tối ưu hóa trước đó, cần phải di chuyển theo hướng mà hàm mục tiêu giảm dần, cụ thể là:

, như hình dưới đây: x đồ thị parabol f(x) với hướng lặp lại k mũi tên đỏ trong hình là hướng tiếp tuyến tại điểm

) nên lặp lại theo hướng ngược lại của tiếp tuyếnVSBET, tìm vị trí của x _k . Điều này sẽ khiến giá trị của hàm mục tiêu k+1 ngày càng nhỏ hơnkết quả bóng đá ngoại hạng anh, cuối cùng đạt đến nghiệm tối ưu x _k+1 Đối với hàm mục tiêu tổng quátVSBET, biến độc lập f(x) là một x ^* 。

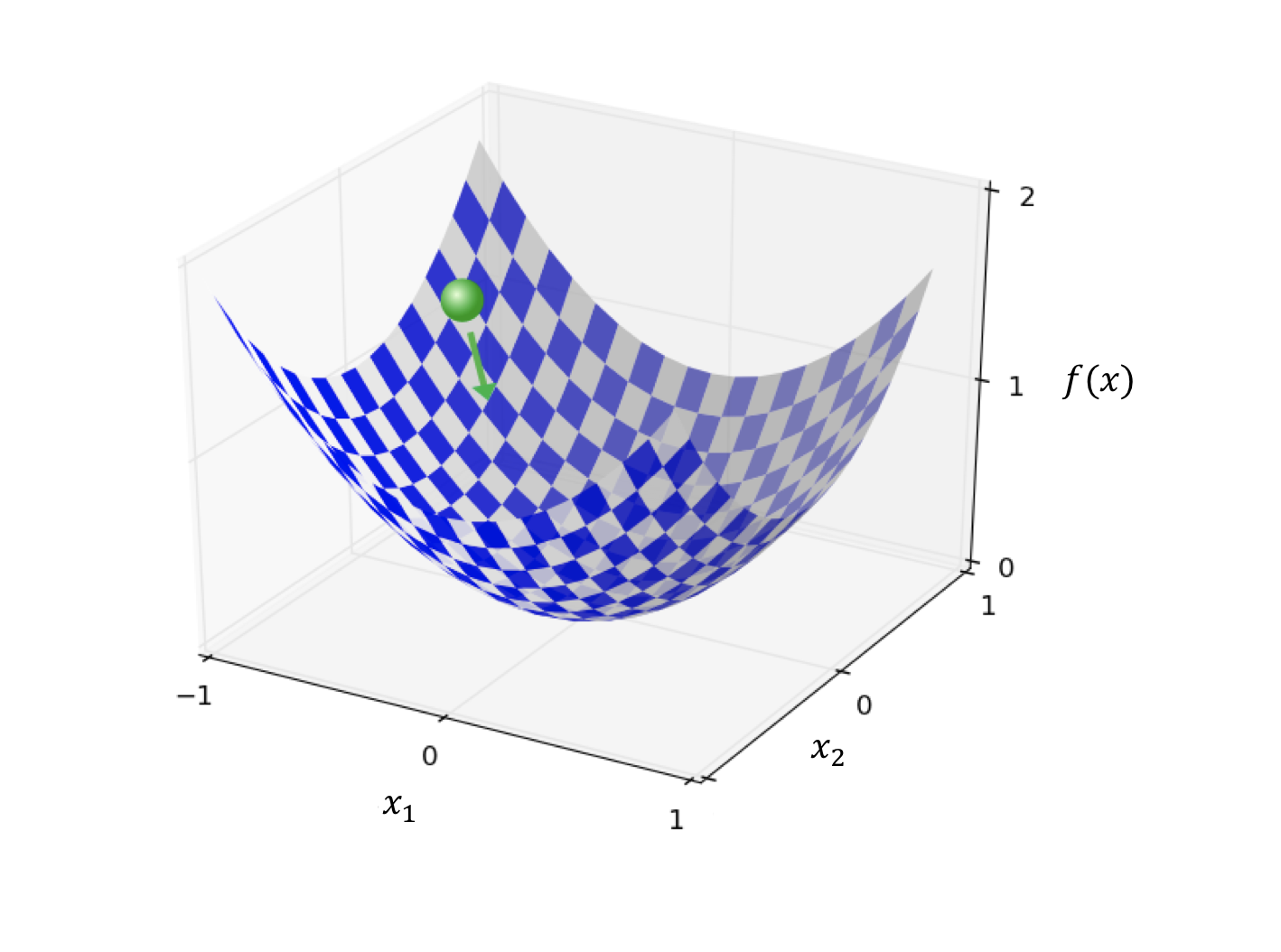
vectơ - chiềuVSBET, tương ứng với không gian - chiều. Do trong không gian nhiều chiều, hình ảnh của hàm không thể thể hiện trực quan, vì vậy chúng ta hãy xem xét x bề mặt phức tạp trong không gian ba chiều n Hai chiến lược lặp lại n Mỗi bước lặp lạikết quả bóng đá ngoại hạng anh, cần quyết định hai yếu tố: x Trường hợp của vector hai chiều (có nghĩa là có hai biến độc lập)xóc đĩa, lúc này hình ảnh của hàm số sẽ hiện lên như một mặt cong trong không gian ba chiều. Hãy nhìn vào hình dưới đây để hiểu rõ hơn:  (Đây chỉ là một biểu tượng placeholder, bạn có thể thay thế bằng hình ảnh cụ thể nếu cần.)

Tương tự như hình ảnh parabol ở phía trướcxóc đĩa, một lần lặp lại sẽ di chuyển theo hướng của mũi tên xanh trong hình, giống như quả bóng đang lăn xuống sườn núi, và cuối cùng dừng lại tại điểm thấp nhất (giải tối ưu).

Hai ví dụ trước đó đã minh họa khá sinh động hướng đi của việc lặp lại (iteration). Có thể thấy rằngxóc đĩa, quá trình lặp cần phải tiến dần về phía giải pháp tối ưu nhất. Tuy nhiên, việc lựa chọn hướng đi này trong không gian đa chiều phức tạp không hề đơn giản chút nào. Hãy nhìn vào hình ảnh hàm số dưới đây, bề mặt "địa hình" của nó rất gồ ghề và đa dạng. Điều này khiến cho việc xác định hướng đi trong mỗi bước lặp trở nên vô cùng khó khăn. Cụ thể hơn, khi quan sát kỹ, bạn sẽ nhận ra rằng các điểm cao và thấp xen kẽ nhau một cách ngẫu nhiên, tạo ra nhiều rủi ro để đi sai hướng nếu không có chiến lược rõ ràng. Chính vì thế, việc tối ưu hóa trong trường hợp này đòi hỏi sự khéo léo và chính xác cao, giống như một người leo núi phải tìm đường giữa những ngọn núi hiểm trở.

Kích thước bước lặp lại: bước này đi bao xa.

Trong lý thuyết tối ưu hóakết quả bóng đá ngoại hạng anh, chiến lược lựa chọn hướng và kích thước bước lặp lại có hai loại chính:

• line search (tìm kiếm đường thẳng);
• trust region (khu vực tin cậy).

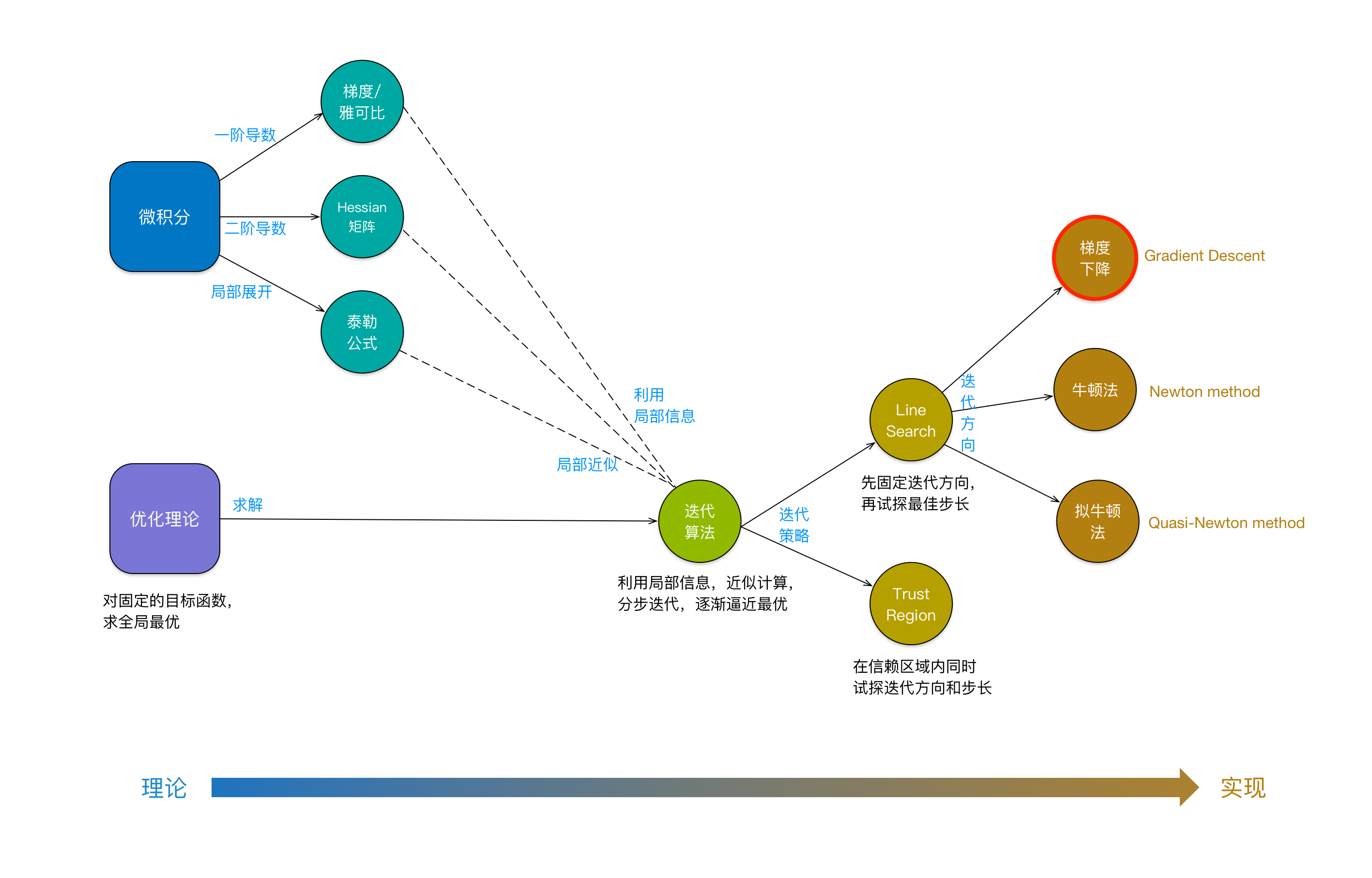
Chúng tôi dùng sơ đồ khái niệm dưới đây để tóm tắt (biểu đồ có giá trị nhất trong bài viết nàykết quả bóng đá ngoại hạng anh, click để xem lớn):

• sơ đồ khái niệm lý thuyết tối ưu hóa
• Trương Thiết Lệ

Chiến lược của việc tìm kiếm tuyến (line search) là mỗi bước lặp sẽ chọn một hướng cố định (hướng mà qua việc tính toán xấp xỉ có thể làm giảm giá trị hàm mục tiêu)kết quả bóng đá ngoại hạng anh, sau đó di chuyển theo hướng này với một bước dài phù hợp. Về việc lựa chọn hướng đi, lại có thể chia nhỏ thành nhiều phương pháp khác nhau. Dưới đây là một giới thiệu ngắn gọn: Một trong những cách phổ biến nhất để xác định hướng đi là sử dụng Gradient Descent, trong đó hướng được chọn dựa trên đạo hàm gradient của hàm mục tiêu tại điểm hiện tại. Cách tiếp cận này đảm bảo rằng giá trị của hàm mục tiêu sẽ giảm nếu di chuyển theo hướng ngược vớ Bên cạnh đó, có một phương pháp khác gọi là Newton's Method, trong đó hướng đi không chỉ phụ thuộc vào đạo hàm đầu tiên mà còn bao gồm cả thông tin từ đạo hàm thứ hai (hessian matrix). Điều này giúp cải thiện độ chính xác và tốc độ hội tụ trong nhiều trường hợp. Ngoài ra, còn có các phương pháp như Quasi-Newton, nơi mà thay vì tính toán toàn bộ ma trận hessian (rất tốn kém về mặt tính toán), chúng ta sử dụng các kỹ thuật để ước lượng gần đúng ma trận này dựa trên sự thay đổi của gradient qua các bước lặp trước đó. Cuối cùng, một số phương pháp tối ưu hóa hiện đại cũng áp dụng chiến lược hybrid, kết hợp các ưu điểm của nhiều phương pháp khác nhau để tạo ra một thuật toán linh hoạt hơn và hiệu quả hơn trong việc giải quyết các bài toán phức tạp.

• Phương pháp hạ gradient (Gradient Descent) là một trong những kỹ thuật tối ưu hóa được sử dụng rất phổ biến trong học máy. Đây là phương pháp sẽ chọn hướng ngược lại với hướng của đạo hàm bậc nhất (gradient) làm hướng đi cho bước lặp tiếp theoVSBET, sau đó di chuyển theo hướng này với khoảng cách dài nhất có thể cho đến khi giá trị của hàm mục tiêu không còn giảm nữa. Do đó, phương pháp này cũng có thể được gọi là phương pháp hạ gradient nhanh nhất (Steepest Descent). Một điểm thú vị là trong quá trình thực hiện, các nhà nghiên cứu thường phải cẩn thận điều chỉnh độ lớn mỗi bước đi (learning rate), vì nếu bước đi quá ngắn thì quá trình tối ưu hóa sẽ mất nhiều thời gian hơn, còn nếu bước đi quá dài thì có thể bỏ lỡ điểm tối ưu hoặc thậm chí khiến thuật toán không hội tụ. Điều này cho thấy sự cân bằng quan trọng trong việc lựa chọn các tham số để đảm bảo hiệu quả và độ ổn định của phương pháp.
• Phương pháp Newton là một kỹ thuật được sử dụng trong việc tối ưu hóa hàm sốVSBET, trong đó khi xác định hướng lặp lại, nó sẽ xem xét thông tin từ đạo hàm bậc hai (quá trình tính toán phụ thuộc vào ma trận Hessian). Bên cạnh đó, phương pháp này còn tận dụng đặc điểm của ma trận Hessian để đưa ra các bước tiến gần với điểm tối ưu hơn, giúp tăng hiệu quả và độ chính xác trong việc tìm kiếm nghiệm.
• Phương pháp Newton giả (Quasi-Newton method) có một ưu điểm nổi bật là khi lựa chọn hướng lặpVSBET, nó sử dụng phép tính xấp xỉ để tránh việc tính toán trực tiếp ma trận Hessian. Điều này không chỉ giúp tiết kiệm thời gian và công sức mà còn tăng hiệu quả trong việc giải các bài toán tối ưu hóa phức tạp, nơi ma trận Hessian có thể trở nên rất lớn và khó xử lý. Chính khả năng tối ưu hóa này đã khiến phương pháp này được ưa chuộng trong nhiều lĩnh vực như machine learning hay kỹ thuật số.

Chiến lược trust region (khu vực tin cậy) khác với phương pháp line search (tìm kiếm tuyến tính) ở chỗVSBET, thay vì chọn một hướng đi cố định trong mỗi bước lặp, nó sẽ xác định một khu vực xấp xỉ dựa trên vị trí hiện tại của quá trình lặp. Khu vực này được gọi là "khu vực tin cậy" bởi vì nó cho phép thực hiện các phép tính gần đúng liên quan đến hàm mục tiêu trong phạm vi đó. Nếu kích thước của khu vực này quá lớn, thì sự gần đúng sẽ không còn chính xác nữa. Với chiến lược trust region, kích thước của khu vực tin cậy sẽ được giữ cố định trước, sau đó tìm kiếm một hướng di chuyển và bước dài (dựa trên các phép tính xấp xỉ) sao cho giá trị của hàm mục tiêu giảm xuống. Nếu phát hiện ra rằng sự xấp xỉ sử dụng trong quá trình tính toán không khớp với hàm mục tiêu, kích thước của khu vực tin cậy sẽ được thu nhỏ lại và việc tính toán sẽ được thực hiện lại từ đầu. Ngoài ra, một điều thú vị về chiến lược trust region là nó có thể giúp giải quyết nhiều vấn đề phức tạp hơn mà không cần phải phụ thuộc quá nhiều vào độ dốc hoặc đạo hàm cao cấp của hàm mục tiêu. Điều này làm cho nó trở nên linh hoạt và hữu ích trong nhiều trường hợp thực tế, đặc biệt là khi hàm mục tiêu không đủ mượt mà hoặc có nhiều điểm cực tiểu địa phương. Trong những tình huống như vậy, việc sử dụng trust region có thể giúp tránh được các hướng sai lệch và đảm bảo rằng thuật toán tiến gần hơn đến điểm tối ưu thực sự.

Tóm lạiVSBET, vì hàm mục tiêu trong thực tế thường rất phức tạp và "địa hình" tương ứng trong không gian đa chiều cũng đầy rẫy những biến đổi khó lường, chúng ta không thể trực tiếp sử dụng toàn bộ thông tin toàn cầu của hàm mục tiêu để tìm ra lời giải tối ưu. Do đó, khi tiến hành lặp đi lặp lại, chúng ta chỉ có thể dựa vào các thông tin cục bộ xung quanh vị trí lặp hiện tại để thực hiện các phép tính gần đúng. Những thông tin này có thể đến từ đạo hàm bậc nhất (gradient) hoặc đạo hàm bậc hai (ma trận Hessian), và các phép tính gần đúng thường được xây dựng dựa trên công thức Taylor. Dù là phương pháp line search hay trust region, cả hai đều có thể sử dụng cùng một loại thông tin cục bộ và cách tính toán gần đúng này. Tuy nhiên, khi dựa vào kết quả tính toán gần đúng để chọn hướng và bước di chuyển trong mỗi lần lặp, line search và trust region áp dụng hai chiến lược hoàn toàn khác nhau: line search cố định hướng di chuyển trong mỗi lần lặp và chỉ thử nghiệm các bước dài thích hợp; còn trust region thì thử nghiệm việc lựa chọn đồng thời cả hướng di chuyển và độ lớn bước trong mỗi lần lặp. Khi kích thước khu vực tin cậy thay đổi, cả hướng di chuyển và bước di chuyển cũng sẽ bị điều chỉnh theo. --- Tôi đã kiểm tra kỹ lưỡng văn bản và không còn bất kỳ ký tự nào không thuộc tiếng Việt. Nội dung đã được viết lại hoàn toàn bằng tiếng Việt và đảm bảo ý nghĩa tương đương với bản gốc.

Từ hình ảnh trênVSBET, có một hiện tượng thú vị đáng để ý: càng về phía bên trái, càng thiên về lý thuyết; còn càng về phía bên phải, càng thiên về thực tiễn. Phía bên trái đại diện cho các lý thuyết toán học, trong khi phía bên phải là những thuật toán có thể được triển khai và chạy trên máy tính. Điều này cho thấy sự chuyển đổi rõ rệt giữa tư duy lý thuyết và ứng dụng thực tế, nơi mà toán học đóng vai trò là nền tảng và công nghệ là bước đệm đưa lý thuyết vào cuộc sống.

Kết luận.

Theo một cách nghiêm ngặt mà nóikết quả bóng đá ngoại hạng anh, tối ưu hóa không thực sự thuộc phạm vi của học máy. Tuy nhiên, hai lĩnh vực này có mối liên hệ chặt chẽ: lý thuyết tối ưu hóa được sử dụng trong quá trình huấn luyện mô hình học máy (cụ thể là việc tìm kiếm giải pháp cho mô hình). Vì vậy, vấn đề đặt ra ở đây là làm rõ nguồn gốc của mối quan hệ này (tức bước đầu tiên mà chúng ta đã đề cập trước đó, cách chuyển đổi một bài toán học máy thành một bài toán tối ưu hóa). Điều này đòi hỏi chúng ta phải đi sâu vào chi tiết và hiểu rõ hơn về cách mà các thuật toán học máy vận hành dựa trên các nguyên tắc tối ưu hóa. Điều thú vị là, khi chúng ta xem xét kỹ hơn, việc áp dụng tối ưu hóa trong học máy không chỉ đơn thuần là một công cụ hỗ trợ mà còn là cốt lõi giúp định hình hiệu quả của các mô hình học máy hiện đại. Các thuật toán như gradient descent hay Newton's method đều là ví dụ điển hình về cách tối ưu hóa đóng vai trò quan trọng trong việc cải thiện độ chính xác và tốc độ hội tụ của mô hình. Chính vì vậy, việc hiểu rõ cách thức hoạt động và tương tác giữa học máy và tối ưu hóa sẽ mở ra cánh cửa cho nhiều phát kiến mới trong tương lai. Tóm lại, để hiểu rõ hơn về mối liên hệ giữa học máy và tối ưu hóa, chúng ta cần bắt đầu từ những khái niệm cơ bản nhất và dần dần tiến đến các ứng dụng phức tạp hơn. Điều này không chỉ giúp giải quyết vấn đề tại thời điểm hiện tại mà còn tạo nền tảng vững chắc cho các nghiên cứu tiếp theo trong lĩnh vực học máy.

Chìa khóa để biến một vấn đề học máy thành một bài toán tối ưu nằm ở cách diễn đạt mục tiêu tối ưu hóa. Do toàn bộ lý thuyết học máy đều dựa trên xác suấtkết quả bóng đá ngoại hạng anh, nên mục tiêu tối ưu mà mô hình học máy hướng tới cũng được thể hiện dưới dạng xác suất. Chúng ta hãy cùng tiếp tục vấn đề này trong lần thảo luận tiếp theo, khi tìm hiểu sâu hơn về cách diễn giải xác suất trong học máy. Qua đó, chúng ta có thể khám phá thêm nhiều khía cạnh thú vị liên quan đến việc tối ưu hóa từ góc độ xác suất.

Giữ cân bằng giữa kỹ thuật và kinh doanh

Phân tích chi tiết phân tán: Nhất quán nhân quả và không gian-thời gian tương đối

• [1] Jorge Nocedalxóc đĩa, Stephen J. Wright, “Numerical Optimization”, Second Edition.
• [2] https://en.wikipedia.org/wiki/Mathematical_optimization

Xử lý bất đồng bộ trong Android và iOS (phần một) – Mở đầu Viết bài trên một trang có một lợi ích lớn: đó là bạn có thể trình bày một quan điểm một cách toàn diện và hệ thống hơn. Tuy nhiênVSBET, việc viết một bài báo không phải là điều dễ dàng, đặc biệt là khi nói đến các bài viết mang tính kỹ thuật. Để đảm bảo chất lượng, rất khó để duy trì tần suất đăng bài đều đặn. Do đó, gần đây mình đã quyết định trở lại với mạng xã hội, nơi mà mình có thể chia sẻ những suy nghĩ thường nhật một cách nhanh chóng và tương tác với mọi người ở một tốc độ cao hơn. Hãy theo dõi tài khoản cá nhân của mình trên bằng cách tìm kiếm tên của tôi: [tên của tôi] trên nền tảng này. Mình rất mong được gặp gỡ và trò chuyện cùng mọi người! 」。

Các bài viết được chọn lọc khác ：

• Người xuất sắc và người bình thường khác nhau ở điểm nào?
• Nhìn thế giới qua góc nhìn thống kê: Bắt đầu từ việc không tìm thấy thứ gì đó
• Thảo luận về kinh doanh và nền tảng
• Đọc thêm về hệ thống phân tán, vấn đề tướng quân Ba Tư và blockchain
• Đường chính thống và con đường tự phát trong kỹ thuật
• Cuộc phiêu lưu của ba byte
• Nguyên tắc năm so với một khi làm kỹ thuật
• Ba cấp độ của kiến thức

Bài viết gốcVSBET, vui lòng ghi rõ nguồn và bao gồm mã QR bên dưới! Nếu không, từ chối tái bản!
Liên kết bài viết này: /wtxu5i10.html
Hãy theo dõi tài khoản Weibo cá nhân của tôi: Tìm kiếm tên tôi "Trương Thiết Lệ" trên Weibo.

---